Creating a simple parser with ANTLR

September 13, 2014

Page content

Recently, I’ve faced a task of developing a tool which allows the application to have base of (not very complex) logical rules. There were three demands:

The rules were to be written by non-programmers, so using of the languages which the program is written in (Java/Scala), wasn’t very good.
The rule base should be changeable without redeployment of the application, ideally, should be stored in a database.
We should have control on compilation and error emission.

The first and the second demand could be met by developing some kind of Scala- or Groovy-based DSL, extremely simple. But I’ve come with several arguments against:

The third requirement might be hard to meet.
The rules are quite simple, so embedding an interpreter of a general-purpose language might be overkill.
The language which rules consumer is written in might be changed (from Java/Scala to Python e.g.)

So, I’ve decided to write a very simple rule parser/compiler. After I’d created a prototype I decided to write this post, hope it’ll be useful. I say in advance that you can see the code adapted for this post in this repository.

The problem

Suppose we have rules like

if condition_1 and condition_2 or condition_3 then conclusion

where conditions are logical expressions which parts can be logical constants (true / false), logical variables (isAmazing), arithmetic expressions with comparison (a+b < 0.42). We want to translate a file consist of such rules into some easy-to-interpret format, store it somewhere and in a time get from another piece of software and evaluate them one-by-one in a specified environment.

The good idea is to store the rules in some form of tree. Consider one rule:

Simple rule tree

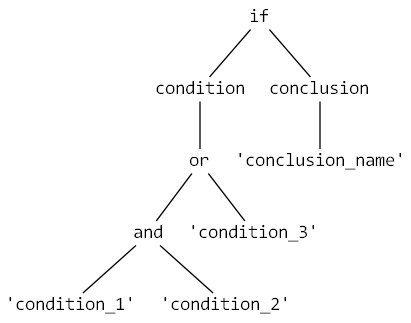
The root node is if, which represents the rule itself, children are condition and conclusion. The condition has a subtree of a logical expression, which leaves are constants or variables. The conclusion is just simply a name of one.

The full file will have zero, one or many such rules united by file root node.

Next, this rule set tree must be serialized in some form to be stored. I’ve decided to use JSON/BSON while performance is satisfactory.

Let’s consider, how to translate a sequence of symbols (a file) into a tree form.

Lexical analysis

How can we translate a file (a stream of bytes/characters) into such a tree? We have a language with two sets of words:

Fixed finite set of “keyword” (if, then, and, or, decimal numbers, arithmetic and comparison operators +, *, <, = etc.)
Infinite set of identifiers of variables and conclusions.

All this words are called tokens and a process of a translation of an input sequence of characters into an output sequence of tokens is named tokenization, lexical analysis or lexing. The process is commonly performed by finite-state machine built with regular expressions.

But I’m not intended to describe the process in details, because it’ll take plenty of time. In the end of the post there is an additional reading list. Though, I’ll describe the building of a tokenizer using special tools.

Parsing

So, we have translated the sequence of characters to the sequence of character groups called tokens, which have far more logical meaning together. The next task is to build a tree of the tokens.

There is a way of specifying how tokens are assembled into legal sentences in a given language – formal grammars. There is heavy theory under formal languages and grammars and I’m certainly not going to retell it, especially with all mathematical strictness, but I’ll give a very simple explanation.

Let’s start from the root, from the file of rules itself. What is it? We said early that the file was zero, one or many rules. Let’s write it a bit formally:

file ->rule* EOF

rule refers to another grammar rule (not written yet) which describes how does rule subtree is built. (Remark: It’s just a coincidence in names; you should distinguish rules of the grammar and rules from the original problem domain.) In theoretical CS and mathematics, the star is called Kleene star and designates “zero, one or many”. EOF stands for “end of file”.

Let’s write the rule for “rule” (oh this pun):

rule -> IF condition THEN conclusion SEMI

There are three symbols in uppercase which stands for according tokens (if, then and ; respectfully). Go deeper:

conclusion -> IDENTIFIER

IDENTIFIER is a token for string identifier which represents a conclusion name.

condition -> logical_expression
logical_expression -> logical_expression AND logical_expression
logical_expression -> logical_expression OR logical_expression
logical_expression -> logical_constant
...

Et cetera to the leaves of the tree.

Now, using this grammar and special parsing algorithms we can transform our sequence of tokens to a tree called a parse tree. As early, I’m not going to describe these algorithms here because they are quite complex and have many shades (see the end of the post for further reading).

ANTLR

How does one create any kind of parser in a modern world not for education purposes (in most cases)? Definitely, using special tools. Lexical analyzer (tokenizer) can be built by a tool called lexical analyzer generator, which work by the following scheme:

User creates a file with special lexical rules which describe how characters should be grouped into tokens. Usually, the file contains pieces of code in a programming language.
Generator reads the files and generates the code of lexical analyzer using rules and pieces of code from the file. There is a great deal of such programs, one of the oldest and most known is lex (and its free software double GNU flex).

What about parsers? There are also parser generators (sometimes called compiler-compilers) which works on the very similar scheme, only using another type of rules – grammar rules. There also plenty of such generators, one of the oldest and most known if yacc (and its free software double GNU bison).

I’ve used a tool named ANTLR. It’s a very modern piece of software, which allows to build combined rule files (lexical and grammar rules together), generates code in Java, Python, C# and other languages and implements advanced parser algorithms which make life simpler (such as left recursion elimination).

Preparations

We’re going to use ANTLR to build a parser and then use the parser to build an AST (abstract syntax tree) from rule sets. I’ll describe everything using Java 1.7 and Maven (I hope you have a clue about Maven; if not, google for beginners’ guide, there are tons of them on the internets).

Let’s create an empty Maven project.

$ mvn archetype:create -DgroupId=me.ivanyu -DartifactId=rule-compiler

Update JUnit version

<dependency>
  <groupId>junit</groupId>
  <artifactId>junit</artifactId>
  <version>4.11</version>
  <scope>test</scope>
</dependency>

Add ANTLR runtime to the dependencies

<dependencies>
...
  <dependency>
    <groupId>org.antlr</groupId>
    <artifactId>antlr4-runtime</artifactId>
    <version>4.3</version>
  </dependency>
...

and ANTLR build source generating plugin:

<build>
...
  <plugins>
...
    <plugin>
      <groupId>org.antlr</groupId>
      <artifactId>antlr4-maven-plugin</artifactId>
      <version>4.3</version>
      <executions>
        <execution>
          <goals>
            <goal>antlr4</goal>
          </goals>
        </execution>
      </executions>
    </plugin>
...

ANTLR plugin gets grammar description from src/main/antlr4/<package>/*.m4 files, generates the code and places it into target/generated-sources/antlr4/<package>. This process can be initialized by invoking generate-sources Maven phase or another phase depends on it (such as compile).

I’ve also set Java version to 1.7:

<plugin>
  <groupId>org.apache.maven.plugins</groupId>
  <artifactId>maven-compiler-plugin</artifactId>
  <version>3.1</version>
  <configuration>
    <source>1.7</source>
    <target>1.7</target>
  </configuration>
</plugin>

ANTLR gives tools to make parser development more comfortable. One of the tools is ANTLRworks. The tool can draw parse trees interactively. Though, I’ve experienced some problems with this functionality (with left recursion mostly) and abandoned using ANTLRworks. Another option is ANTLR v4 grammar plugin for IntelliJ IDEA which works perfectly (I’m sure that there are plugins for another IDEs too).

Now technically we’re ready to write code.

The language

Let’s start from the language description. Create file src/main/antlr4/<your package name>/RuleSetGrammar.g4 with the following content:

grammar RuleSetGrammar;

In my case the package is named me.ivanyu.

Now the application skeleton is created, you could run mvn compile or mvn generate-sources.

ANTLR enables programmers to write united lexical and grammar rule files. Let’s write lexical rules first:

grammar RuleSetGrammar;

/* Lexical rules */

IF   : 'if' ;
THEN : 'then';

AND : 'and' ;
OR  : 'or' ;

TRUE  : 'true' ;
FALSE : 'false' ;

MULT  : '*' ;
DIV   : '/' ;
PLUS  : '+' ;
MINUS : '-' ;

GT : '>' ;
GE : '>=' ;
LT : '<' ;
LE : '<=' ;
EQ : '=' ;

LPAREN : '(' ;
RPAREN : ')' ;

// DECIMAL, IDENTIFIER, COMMENTS, WS are set using regular expressions

DECIMAL : '-'?[0-9]+('.'[0-9]+)? ;

IDENTIFIER : [a-zA-Z_][a-zA-Z_0-9]* ;

SEMI : ';' ;

// COMMENT and WS are stripped from the output token stream by sending
// to a different channel 'skip'

COMMENT : '//' .+? ('\n'|EOF) -> skip ;

WS : [ \r\t\u000C\n]+ -> skip ;

The lexical rules are written uppercase. Using them the tokenizer will be generated. I think the rules is pretty straightforward, only a couple of places does possibly need clarifications which is given in the comments.

The grammar rules follow:

/* Grammar rules */

rule_set : single_rule* EOF ;

single_rule : IF condition THEN conclusion SEMI ;

condition : logical_expr ;
conclusion : IDENTIFIER ;

logical_expr
 : logical_expr AND logical_expr # LogicalExpressionAnd
 | logical_expr OR logical_expr  # LogicalExpressionOr
 | comparison_expr               # ComparisonExpression
 | LPAREN logical_expr RPAREN    # LogicalExpressionInParen
 | logical_entity                # LogicalEntity
 ;

comparison_expr : comparison_operand comp_operator comparison_operand
                    # ComparisonExpressionWithOperator
                | LPAREN comparison_expr RPAREN # ComparisonExpressionParens
                ;

comparison_operand : arithmetic_expr
                   ;

comp_operator : GT
              | GE
              | LT
              | LE
              | EQ
              ;

arithmetic_expr
 : arithmetic_expr MULT arithmetic_expr  # ArithmeticExpressionMult
 | arithmetic_expr DIV arithmetic_expr   # ArithmeticExpressionDiv
 | arithmetic_expr PLUS arithmetic_expr  # ArithmeticExpressionPlus
 | arithmetic_expr MINUS arithmetic_expr # ArithmeticExpressionMinus
 | MINUS arithmetic_expr                 # ArithmeticExpressionNegation
 | LPAREN arithmetic_expr RPAREN         # ArithmeticExpressionParens
 | numeric_entity                        # ArithmeticExpressionNumericEntity
 ;

logical_entity : (TRUE | FALSE) # LogicalConst
               | IDENTIFIER     # LogicalVariable
               ;

numeric_entity : DECIMAL              # NumericConst
               | IDENTIFIER           # NumericVariable
               ;

The rule order matters: it determines the order or rules tries. It especially important in setting operators precedence (and must be applied before or, * – before + etc.)

Texts after # sign are labels which are used to tell different appearances of the rules apart.

Some rules are left recursive (have the first symbol in the right part of a rule equals the left part of the rule) and most parsing algorithms can’t deal with such rules directly – left recursion elimination techniques are required. But ANTLR gives you the ability to write left recursive rules and processes them correctly, so the grammar becomes much simpler.

Having this file we can do code generation (mvn generate-sources). You can visit /target/generated-sources/antlr4 and examine the generated code. Classes are ready to use but do nothing useful, except the lexer, which can do tokenization right now.

In our case ANTLR generates six files: two identical files with token constants, the lexer in a class file RuleSetGrammarLexer.class, the parser in a class file RuleSetGrammarParser.class and RuleSetGrammarListener interface and its empty implementation RuleSetGrammarBaseListener. Listeners’ methods are used when the parser traverses through the parse tree (in depth-first order) as callbacks for different events such as “a node of a particular type entered” or “… exited”. There is more powerful instrument called walkers which gives control of traverse itself (see ANTLR documentation).

Testing

Our piece of software requires proper testing. First of all we should test whether the lexer and the parser distinguish correct and incorrect rule sets. Looking to the grammar we can say:

The rules have prescribed form.
A conclusion is a single identifier.
A condition is a logical expression.
A logical expression can be two logical expressions combined with a logical operator (and/or), a comparison expression, a logical expression in parenthesis, or a logical entity.
A comparison expression can be two operands combined with comparison operator or a comparison expression in parenthesis.
A comparison operand is an arithmetic expression.
An arithmetic expression can be two arithmetic expressions combined with an arithmetic operator, an arithmetic expression with negation, an arithmetic expression in parenthesis and a numeric entity.
A numeric entity can be a decimal number (constant) or an identifier (numeric variable).
A logical entity can be a logical constant (true/false) or an identifier (logical variable).

Using these rules, plenty of test cases can be written and examined using a test framework (I’ve used JUnit). We only need to teach the parser to throw exceptions on errors which is done with custom error handling strategy (code). (See full test code.)

AST generation

AST stands for abstract syntax tree. It is very similar to parse tree, but lies on a higher layer of abstraction. It doesn’t contain various service nodes necessary for convenient parser generation and container node might be more suitable for further using.

I’ve create AST to be serialized to JSON/BSON using Java library Jackson, so I’ve created classes and interfaces (simple POJOs – plain old Java objects) to represent AST nodes and have supplemented them with Jackson annotations such as @JsonProperty.

The main idea of AST generation using ANTLR’s listeners is to use stacks. Stacks are you first mate when you’re dealing with broad class of problems on trees. Example: we have a subtree of and:

Here is the traverse order schema:

Traverse order

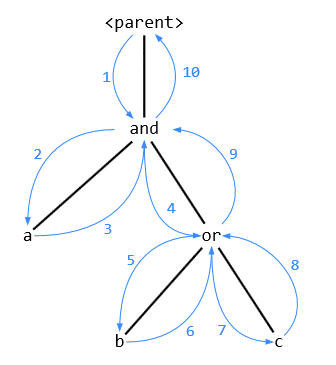
Enter and.
Enter a.
Exit a.
Enter or.
Enter b.
Exit b.
Enter c.
Exit c.
Exit or.
Exit and.

We create a stack for operands of logical expressions. When we leave the logical operand, we put it onto the stack. When we leaves logical operator, we pop top two values from the logical operands stack, combines them into a logical expression with the operator and put the result back onto the stack. Our grammar guarantees that there will be no problem with absence or redundant elements on the stacks (if our listener code isn’t buggy, of course). (See full listener code.)

Now, when we have the AST, we can serialize it to JSON/BSON format using Jackson library and then store and use it (interpret) when it’s needed.

The AST generation can (and should) be tested, also. There are some approaches to creating test cases. I’ve preferred to construct a target result set for each case by hand using helper functions and then compare the target test set and result sets got from compilation using standard overridden “equals” method. (See full test code.)

Further work

The parser/compiler is mostly complete, but need some important improvements. The first improvement is to provide user with proper error messages like in good compilers. The second is to enable error recovery: if there is an error in a rule, report it and continue to the next instead of full stop. More testing should be done also.

Additional reading

If you want to study deeper, I can recommend you a bit of material:

“The Definitive ANTLR 4 Reference” by Terence Parr, ANTLR’s creator.
“Compilers: Principles, Techniques, and Tools” by A. V. Aho, M. S. Lam, R. Sethi, J. D. Ullman, absolutely comprehensive and classical.
Coursera course “Compilers” by Alex Aiken, totally great.

Thank you for your attention.