Z algorithm
Introduction
There are some algorithms of exact substring searching (e.g. Knuth-Morris-Pratt, Boyer-Moore etc.) I want to explain one of them which is called Z algorithm in some sources.
Z-boxes and Z-values
Let’s consider the concept of Z-box. Take the string S = “abcxxxabyyy”. We have an internal part “ab” in the string which repeats its prefix. The internal “ab” is a Z-box. It has the beginning at the position with index 6 and the end in 7 (0-based). Z-boxes are substrings which match string prefixes with the same length. For the Z-box, let’s call the corresponding prefix the prototype (it’s my term but I think it’s OK to use it.)
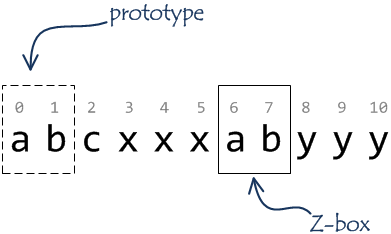
In fact, the string “abcxxxabyyy” has three non-empty (i.e. with length greater than zero) Z-boxes:
- the whole strings matches it’s prefix length 11;
‘a’character at the position 6;- just considered substring
“ab”(6-7).
Let Z-value, Zi(S) or just Zi be the length of a Z-box in string S which starts at the position i. Obviously, Z-value can’t be bigger than the length of the rest of the string.
We can compute all Z-values in the string:
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Character | a | b | c | x | x | x | a | b | y | y | y |
| Z-value | 11 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 |
Z-box [0-10] matches the whole string, so has the length 11. Z-box [6-7] matches prefix [0-1], length 2. Z-box [7-7] matches prefix [0-0], length 1.
Let’s ignore empty Z-boxes (with the length 0).
Some examples:
| Index | 0 | 1 | 2 | 3 | 4 | 5 |
| Character | a | a | a | a | a | a |
| Z-value | 6 | 5 | 4 | 3 | 2 | 1 |
| Index | 0 | 1 | 2 | 3 | 4 |
| Character | a | b | b | b | b |
| Z-value | 6 | 0 | 0 | 0 | 0 |
| Index | 0 | 1 | 2 | 3 | 4 | 5 |
| Character | a | b | c | a | b | c |
| Z-value | 6 | 0 | 0 | 3 | 0 | 0 |
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Character | a | b | r | a | c | a | d | a | b | r | a |
| Z-value | 11 | 0 | 0 | 1 | 0 | 1 | 0 | 4 | 0 | 0 | 1 |
Naïve computation of Z-values
The naïve algorithm of Z-values computation is very simple: we just need to go through all string indexes starting from 1 and explicitly calculate Zi(S).
In Python it’d look like:
def z_naive(s):
Z = [len(s)]
for k in range(1, len(s)):
n = 0
while n + k < len(s) and s[n] == s[n + k]:
n += 1
Z.append(n)
return ZOr you might want some Python magic :)
Z = [len(list(takewhile(lambda p: p[0] == p[1], zip(s, s[k:]))))
for k in range(len(s))]But simple is better than complex, isn’t it?
Advanced computation of Z-values
The naïve implementation has O(|S|2) time complexity, where |S| is the length of the string. Can it be better? Yes, it can.
What do we know about Z-box? We know that the corresponding substring is exactly the same as the prefix of the string (with the same length). We compute Z-value sequentially from the beginning, so we could use these previous values.
Introduce indexes lti (for “left”) and rti (for “right”). rti indicates the right-most end (the index of the last character) of any Z-box that starts at the position i or to the left of this position at the position lti. In the future we will skip i in lti and rti. Let’s call Z-box in range [lt..rt] (both ends are included) the current Z-box.
For index k inside the current Z-box, let’s call index p=k-lt lying inside the prototype the pair index.
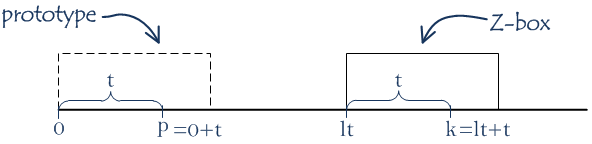
We know the value of Zp. Substrings in Z-box and its prototype are equal. Can we say that Zk = Zp? Under some conditions, yes.
The fact that the current character at the position k is inside previously found Z-box can give us some information. Let’s take substring S(k..rt) and consider two cases.
Case 1
Zp < |S(k..rt)|, i.e. Zp is less then the length of the rest (starting from k) of the current Z-box.
|S(k..rt)| = rt-k+1.
We can add k to the both side of the condition: k+Zp < rt+1.
Note: Pay attention that if we have a string with the length n which starts at the position i then the end of the string will be at the position n+i-1. For example, if n=1 and i=2 then the string begins and ends at the position 2. If i=0 and n=2 then the string begins in 0 and ends in 1.
In this case, we have two identical substrings (Z-box and its prototype), two identical characters inside them (at k and p positions correspondingly).
Moreover, we have the following information:
- substrings
S(p..p+Zp-1)andS(0..Zp-1)are identical (from the meaning ofZp); - substrings
S(k..k+Zp-1)andS(p..p+Zp-1)are identical because indexeskandk+Zp-1,pandp+Zp-1lie inside the Z-box and its prototype at the same relative positions; - substrings
S(k..k+Zp-1)andS(0..Zp-1)are identical (from statement 1 and 2);
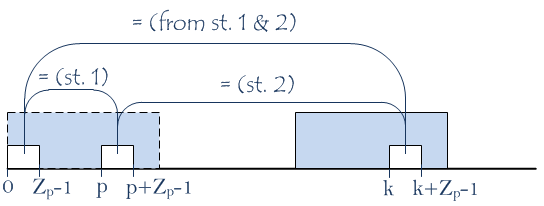
- characters
S(p+Zp)andS(Zp)aren’t equal (again, from the meaning ofZp); - characters
S(k+Zp)andS(p+Zp)are equal because these indexes lie inside Z-box and its prototype at the same relative positions; - characters
S(k+Zp)andS(Zp)aren’t equal (from statement 4 and 5);
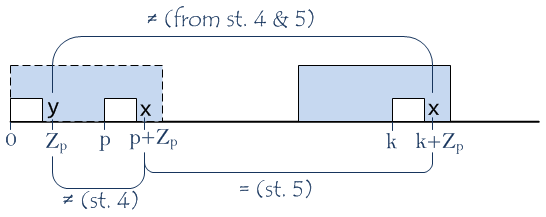
From statements 3 and 5 and the meaning of Zk we can conclude that Zk is equal to Zp.
Thus we can state that when index k is inside the current Z-box with the left border lt, right border rt and Zp < rt-k+1 then Zk = Zp, where p=k-lt.
lt and rt remain the same because k+Zk certainly lies to the left of the current rt.
We need the strict condition Zp < |S(k..rt)| instead of Zp ≤ |S(k..rt)| to be able to say about the equality of characters S(k+Zp) and S(p+Zp) with confidence. If Zp = |S(k..rt)| then S(k+Zp) lies outside the current Z-box and we have no idea about either these characters are equal or not. Why don’t we just check? This smoothly brings us to the case 2.
Case 2
Zp > |S(k..rt)|.
|S(k..rt)| = rt-k+1.
In this case we can’t simply state that Zk = Zp because we don’t know anything about equality of characters beyond the right bounds of prototype and Z-box.
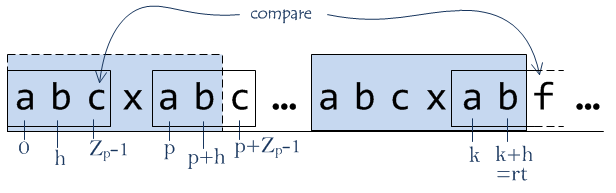
We know that substrings S(k..k+h), S(p..p+h) and S(0..h) are identical. We can simply compare characters from ranges [rt+1..|S|] and [rt-k+1..|S|-k] until the first inequality or the end of the ranges (and the whole string). If we found not equal characters at positions q and k+q then Zk equals the length of the equal substrings, i.e. Zk = q.
Of course, we must set the new value to rt and lt, corresponding to the newly found Z-box because k+q-1 lies to the right of rt (or at least they are equal).
Obviously, when k isn’t inside the current Z-box (k > rt), we have to calculate Zk explicitly.
The formalization of the algorithm might look like this:
Having string S,
Set Z0=|S|, lt=0, rt=0.
For each k, 1 ≤ k < |S| do:
- If
k > rt: calculateZk(S)explicitly. IfZk > 0, setlt := kandrt := k+Zk-1. - Else:
p := k-lt.
2.1. IfZp < rt-k+1, setZk := Zp.
2.2. IfZp ≥ rt-k+1, for eachi,rt+1 ≤ i < |S|do:
2.2.1. IfS(i) = S(i-k): incrementiand continue.
2.2.2. IfS(i) ≠ S(i-k): setZk := i-k,lt := k,rt := i-1and break.
And in Python:
def z_advanced(s):
"""An advanced computation of Z-values of a string."""
Z = [0] * len(s)
Z[0] = len(s)
rt = 0
lt = 0
for k in range(1, len(s)):
if k > rt:
# If k is outside the current Z-box, do naive computation.
n = 0
while n + k < len(s) and s[n] == s[n+k]:
n += 1
Z[k] = n
if n > 0:
lt = k
rt = k+n-1
else:
# If k is inside the current Z-box, consider two cases.
p = k - lt # Pair index.
right_part_len = rt - k + 1
if Z[p] < right_part_len:
Z[k] = Z[p]
else:
i = rt + 1
while i < len(s) and s[i] == s[i - k]:
i += 1
Z[k] = i - k
lt = k
rt = i - 1
return ZExample
Let’s consider the example: take the string S = “ababxababyabaca” and calculate Z-values by the described algorithm.
We’ll highlight the current Z-box with the blue color in the “Index” row and matching and non-matching characters of a potential Z-box with the green and the red color respectively in the “Character” row.
Z0 = |S| = 15.
Start from k = 1. lt = 0, rt = 0.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | ||||||||||||||
| k |
k=1 > rt=0 and we must calculate Z1 explicitly. S(1) ≠ S(0), so Z1 = 0. We don’t treat empty Z-boxes as normal Z-boxes, so we just skip it, no updates of lt and rt are made.
k = 2, lt = 0, rt = 0.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | |||||||||||||
| k |
Again, k=1 > rt=0 and we’re calculating Z2 explicitly. S(2) = S(0), S(3) = S(1), S(4) ≠ S(2), so Z2 = 2. This is a normal newly found Z-box and we update lt := k = 2, rt := k + Zk - 1 = 2 + 2 - 1 = 3.
k = 3, lt = 2, rt = 3.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | 2 | ||||||||||||
| lt | rt | ||||||||||||||
| p | k |
Here, k=3 ≤ rt=3. It has the pair index p = k-lt = 3-2 = 1. Zp=Z1=0. Z1 < rt-k+1=1, so we don’t need to examine any additional characters and can say that Z3 = 0.
k = 4, lt = 2, rt = 3.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | 2 | 0 | |||||||||||
| lt | rt | ||||||||||||||
| k |
k=4 > rt=3 and we’re calculating Z4 explicitly. S(4) ≠ S(0), so Z4 = 0.
k = 5, lt = 2, rt = 3.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | 2 | 0 | 0 | ||||||||||
| lt | rt | ||||||||||||||
| k |
k=5 > rt=3 and we’re calculating Z5 explicitly. Z5 = 4. This is a normal newly found Z-box and we update lt := k=5, rt := k+Zk-1 = 5+4-1 = 8.
k = 6, lt = 5, rt = 8.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | 2 | 0 | 0 | 4 | |||||||||
| lt | rt | ||||||||||||||
| p | k |
k=6 ≤ rt=8. The pair index p = k-lt = 6-5 = 1. Zp = Z1 = 0. Z1 < rt-k+1 = 3, so we don’t need to examine any additional characters and can say that Z6 = 0.
k = 7, lt = 5, rt = 8.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | 2 | 0 | 0 | 4 | 0 | ||||||||
| lt | rt | ||||||||||||||
| p | k |
k=7 ≤ rt=8. The pair index p = k-lt = 7-5 = 2. Zp = Z2 = 2. Z2 ≥ rt-k+1=2, so we need to examine characters starting from rt+1=9 and compare them to characters starting from rt+1-k=2. S(9) ≠ S(2), first not equal characters are at positions 2 and 9. So, Z7 = 9-k = 2. Also, we need to update lt := k=7, rt := k+Zk-1 = 7+2-1 = 8.
k = 8, lt = 7, rt = 8.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | 2 | 0 | 0 | 4 | 0 | 2 | |||||||
| lt | rt | ||||||||||||||
| p | k |
k=8 ≤ rt=8. The pair index p = k-lt = 8-7 = 1. Zp = Z1 = 0. Z1 < rt-k+1 = 1, so we don’t need to examine any additional characters and can say that Z8 = 0.
k = 9, lt = 7, rt = 8.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | 2 | 0 | 0 | 4 | 0 | 2 | 0 | ||||||
| lt | rt | ||||||||||||||
| k |
k=9 > rt=8 and we’re calculating Z9 explicitly. S(9) ≠ S(0), so Z9 = 0.
k = 10, lt = 7, rt = 8.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | 2 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | |||||
| lt | rt | ||||||||||||||
| k |
k=10 > rt=8 and we’re calculating Z10 explicitly. S(10) = S(0), S(11) = S(1), S(12) = S(2), S(13) ≠ S(3), so Z10 = 3. Also, we need to update lt := k=10, rt := k+Zk-1 = 10+3-1 = 12.
k = 11, lt = 10, rt = 12.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | 2 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | 3 | ||||
| lt | rt | ||||||||||||||
| p | k |
k=11 ≤ rt=12. The pair index p = k-lt = 11-10 = 1. Zp = Z1 = 0. Z1 < rt-k+1=2, so we don’t need to examine any additional characters and can say that Z11 = 0.
k = 12, lt = 10, rt = 12.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | 2 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | 3 | 0 | |||
| lt | rt | ||||||||||||||
| p | k |
k=12 ≤ rt=12. The pair index p = k-lt = 12-10 = 2. Zp=Z2=2 ≥ rt-k+1=1, so we need to examine additional characters starting from rt+1=13 and compare them to characters starting from rt+1-k=1. S(13) ≠ S(1), first not equal characters are at positions 1 and 13. So, Z12 = 13-k = 1. Also, we need to update lt := k=12, rt := k+Zk-1 = 12+1-1 = 12.
k = 13, lt = 12, rt = 12.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | 2 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | 3 | 0 | 1 | ||
| lt rt | |||||||||||||||
| k |
k=13 > rt=12 and we’re calculating Z13 explicitly. S(13) ≠ S(0), so Z13 = 0.
k = 14, lt = 12, rt = 12.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | 2 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | 3 | 0 | 1 | 0 | |
| lt rt | |||||||||||||||
| k |
k=14 > rt=12 and we’re calculating Z14 explicitly. S(14) = S(0), so Z14 = 1.
Finally, we have:
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Character | a | b | a | b | x | a | b | a | b | y | a | b | a | c | a |
| Z-value | 15 | 0 | 2 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | 3 | 0 | 1 | 0 | 1 |
Complexity
Let’s find out (not very strictly) time and space complexity of the algorithm. We have |S| iterations. In each iteration we either already have got a Z-value or we have to do some comparisons. When we find q matches during the comparisons rt will be moved to the right: rtk := rtk-1+q. After each mismatch an iteration finishes, so there aren’t more than |S| mismatches. We have not more than |S| iterations with not more than |S| matches and mismatches as a whole. So, the algorithm has O(|S|) time complexity.
Obviously, it requires O(|S|) space to store Z-values.
Search algorithm
You could ask why we need these Z-values at all. This is an appropriate question :) We can use the idea of Z-values for doing a substring search.
Take a string T (for “text”) and a string P (for “pattern”), both built of characters of some alphabet A. Also, take character ’$’ which is not in A. This character is called the sentinel. Assemble all these things in the following way: P$T.
Compute Z-values of this composite string by the advanced algorithm described earlier. All this values will be limited to |P| (except Z0, of course) because of the sentinel which can’t be found at any place in P or T. And when you see a Zj = |P| then you can be sure that substring T(j..j+|P|-1) is an occurrence of P in T. And vice versa: you can be confident that all occurrences will be marked in the list of Z-values.
Let’s consider an example. P = "ab", T = "xaybzabxaby":
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Character | a | b | $ | x | a | y | b | z | a | b | x | a | b | y |
| Z-value | 14 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 0 | 0 |
Even with overlapping matches: P = "aa", T = "xaaay":
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Character | a | a | $ | x | a | a | a | y |
| Z-value | 8 | 1 | 0 | 0 | 2 | 2 | 1 | 0 |
This search algorithm has the O(|P|+|T|) time and space complexity because it has the longest, dominating part – search of Z-values which is O(|S|), |S|=|P|+|T|.
Good algorithm. But there is an obstacle for a general-purpose use: the choice of the sentinel. In some applications you have a short known alphabet. For example, in bioinformatics there are symbols ‘A’, ‘C’, ‘G’ and ‘T’ and we can simply use ’$’ as the sentinel. But what about general Unicode strings?
Search algorithm without the sentinel
Fortunately, there is search algorithm that doesn’t need to use sentinels. The idea is in calculating Z-values of a string PT with a simple modification: after each Z-value is calculated, limit it to the |P|, i.e., Zk := min{|P|, Zk}. This limitation plays role of the sentinel.
The Python code:
def search_without_sentinel(pattern, text):
"""Search without the sentinel."""
s = pattern + text
Z = [0] * len(s)
Z[0] = len(s)
rt = 0
lt = 0
occurrence = []
for k in range(1, len(s)):
if k > rt:
n = 0
while n + k < len(s) and s[n] == s[n+k]:
n += 1
Z[k] = n
if n > 0:
lt = k
rt = k+n-1
else:
p = k - lt
right_part_len = rt - k + 1
if Z[p] < right_part_len:
Z[k] = Z[p]
else:
i = rt + 1
while i < len(s) and s[i] == s[i - k]:
i += 1
Z[k] = i - k
lt = k
rt = i - 1
Z[k] = min(len(pattern), Z[k])
# An occurence found.
if Z[k] == len(pattern):
occurrence.append(k - len(pattern))
return occurrenceAll the code can be found in this repository.
Thank you.